
Maple provides a state-of-the-art environment for algebraic computations in Physics, with emphasis on ensuring that the computational experience is as natural as possible. The theme of the Physics project for Maple 2018 has been the consolidation of the functionality introduced in previous releases, together with significant enhancements, mainly in the handling of differential (quantum or not) tensorial operators, new ways to minimize the number of tensor components taking its symmetries into account, automatic handling of collision of indices in tensorial expressions, automatic setting of the EnergyMomentum tensor when loading solutions to Einstein's equations from the database of solutions, automatic setting of the algebras for the Dirac, Pauli and Gell-Mann matrices when Physics is loaded, simplification of Dirac matrices, a new package Physics:-Cactus related to Numerical Relativity and several other improvements.
Taking all together, there are more than 300 enhancements throughout the entire package, increasing robustness, versatility and functionality, extending once more the range of Physics-related algebraic computations that can be done using computer algebra software, and in a natural way.
As part of its commitment to providing the best possible environment for algebraic computations in Physics, Maplesoft launched a Maple Physics: Research and Development web site with Maple 18, which enabled users to download research versions, ask questions, and provide feedback. The results from this accelerated exchange with people around the world have been incorporated into the Physics package in Maple 2018.
The design of products of tensorial expressions that have contracted indices got enhanced. The idea: repeated indices in certain subexpressions are actually dummies. So suppose ![]() and
and ![]() are tensors, then in
are tensors, then in ![]() ,
, ![]() is just dummy, therefore
is just dummy, therefore ![]() is a well defined object. The new design automatically maps input like
is a well defined object. The new design automatically maps input like ![]() into
into ![]() .
.
| > |
| > |
| (1) |
| > |
| (2) |
This shows the automatic handling of collision of indices
| > |
| (3) |
| > |
| (4) |
Consider now the case of three tensors
| > |
| (5) |
| > |
| (6) |
The product above has indeed the index ![]() repeated more than once, therefore none of its occurrences got automatically transformed into contravariant in the output, and Check detects the problem interrupting with an error message
repeated more than once, therefore none of its occurrences got automatically transformed into contravariant in the output, and Check detects the problem interrupting with an error message
| > |
| Error, (in Physics:-Check) wrong use of the summation rule for repeated indices: `a repeated 3 times`, in A[a]*B[a]*C[a] |
However, it is now also possible to indicate, using parenthesis, that the product of two of these tensors actually form a subexpression, so that the following two tensorial expressions are well defined, where the dummy is automatically replaced making that explicit
| > |
| (7) |
| > |
| (8) |
This change in design makes concretely simpler the use of indices in that it eliminates the need for manually replacing dummies. For example, consider the tensorial expression for the angular momentum in terms of the coordinates and momentum vectors, in 3 dimensions
| > |
| (9) |
Define ![]() respectively representing angular and linear momentum
respectively representing angular and linear momentum
| > |
| (10) |
Introduce the tensorial expression for ![]()
| > |
| (11) |
The left-hand side has one free index, ![]() , while the right-hand side has two dummy indices
, while the right-hand side has two dummy indices ![]() and
and ![]()
| > |
| (12) |
If we want to compute![]() we can now take the square of
we can now take the square of ![]() directly, and the dummy indices on the right-hand side are automatically handled, there is now no need to manually substitute the repeated indices to avoid their collision
directly, and the dummy indices on the right-hand side are automatically handled, there is now no need to manually substitute the repeated indices to avoid their collision
| > |
| (13) |
The repeated indices on the right-hand side are now ![]()
| > |
| (14) |
A new keyword in Setup: differentialoperators, allows for defining differential operators (not necessarily linear) with respect to indicated differentiation variables, so that they are treated as noncommutative operands in products, as we do with paper and pencil. These user-defined differential operators can also be vectorial and/or tensorial or inert. When desired, one can use Library:-ApplyProductOfDifferentialOperators to transform the products in the function application of these operators. This new functionality is a generalization of the differential operators ![]() and
and ![]() , and can used beyond Physics.
, and can used beyond Physics.
A new routine Library:-GetDifferentiationVariables also acts on a differential operator and tells who are the corresponding differentiation variables
Example:
In Quantum Mechanics, in the coordinates representation, the component of the momentum operator along the x axis is given by the differential operator
![]()
The purpose of the exercises below is thus to derive the commutation rules, in the coordinates representation, between an arbitrary function of the coordinates and the related momentum, departing from the differential representation
![]() ;
;
![]()
| > |
Start setting the problem:
| > |
 |
(15) |
Assuming ![]() is a smooth function, the idea is to apply the commutator
is a smooth function, the idea is to apply the commutator ![]() to an arbitrary ket of the Hilbert space
to an arbitrary ket of the Hilbert space ![]() , perform the operation explicitly after setting a differential operator representation for
, perform the operation explicitly after setting a differential operator representation for ![]() , and from there get the commutation rule between
, and from there get the commutation rule between ![]() and
and ![]() .
.
Start introducing the commutator, to proceed with full control of the operations we use the inert form %Commutator
| > |
| > |
| (16) |
| > |
| (17) |
For illustration purposes only (not necessary), expand this commutator
| > |
| (18) |
Note that ![]() ,
, ![]() and the ket
and the ket ![]() are operands in the products above and that they do not commute: we indicated that the coordinates
are operands in the products above and that they do not commute: we indicated that the coordinates ![]() are the differentiation variables of
are the differentiation variables of ![]() . This emulates what we do when computing with these operators with paper and pencil, where we represent the application of a differential operator as a product operation.
. This emulates what we do when computing with these operators with paper and pencil, where we represent the application of a differential operator as a product operation.
This representation can be transformed into the (traditional in computer algebra) application of the differential operator when desired, as follows:
| > |
| (19) |
Note that, in ![]() , the application of
, the application of ![]() is not expanded: at this point nothing is known about
is not expanded: at this point nothing is known about ![]() , it is not necessarily a linear operator. In the Quantum Mechanics problem at hands, however, it is. So give now the operator
, it is not necessarily a linear operator. In the Quantum Mechanics problem at hands, however, it is. So give now the operator ![]() an explicit representation as a linear vectorial differential operator (we use the inert form %Nabla,
an explicit representation as a linear vectorial differential operator (we use the inert form %Nabla, ![]() , to be able to proceed with full control one step at a time)
, to be able to proceed with full control one step at a time)
| > |
| (20) |
The expression (19) becomes
| > |
| (21) |
Activate now the inert operator ![]() and simplify taking into account the algebra rules for the coordinate operators
and simplify taking into account the algebra rules for the coordinate operators ![]()
| > |
| (22) |
To make explicit the gradient in disguise on the right-hand side, factor out the arbitrary ket ![]()
| > |
| (23) |
Combine now the expanded gradient into its inert (not-expanded) form
| > |
| (24) |
Since ![]() is true for all
is true for all![]() , this ket can be removed from both sides of the equation. One can do that either taking coefficients or multiplying by the "formal inverse" of this ket, arriving at the (expected) form of the commutation rule between
, this ket can be removed from both sides of the equation. One can do that either taking coefficients or multiplying by the "formal inverse" of this ket, arriving at the (expected) form of the commutation rule between ![]() and
and ![]()
| > |
| (25) |
The computation rule for position and momentum, this time in tensor notation, is performed in the same way, just that, additionally, specify that the space indices to be used are lowercase Latin letters, and set the relationship between the differential operators and the coordinates directly using tensor notation.
You can also specify that the metric is Euclidean, but that is not necessary: the default metric of the Physics package, a Minkowski spacetime, includes a 3D subspace that is Euclidean, and the default signature, (- - - +), is not a problem regarding this computation.
| > |
| > |
 |
(26) |
Define now the tensor ![]()
| > |
| (27) |
Introduce now the Commutator, this time in active form, to show how to reobtain the non-expanded form at the end by resorting the operands in products
| > |
| (28) |
Expand first (not necessary) to see how the operator ![]() is going to be applied
is going to be applied
| > |
| (29) |
Now expand and directly apply in one ago the differential operator ![]() ;
;
| > |
| (30) |
Introducing the explicit differential operator representation for ![]() , here again using the inert
, here again using the inert ![]() to keep control of the computations step by step
to keep control of the computations step by step
| > |
| (31) |
The expanded and applied commutator (30) becomes
| > |
| (32) |
Activate now the inert operators ![]() and simplify taking into account Einstein's rule for repeated indices
and simplify taking into account Einstein's rule for repeated indices
| > |
| (33) |
Since the ket ![]() is arbitrary, we can take coefficients (or multiply by the formal Inverse of this ket as done in the previous section). For illustration purposes, we use Coefficients and note how it automatically expands the commutator
is arbitrary, we can take coefficients (or multiply by the formal Inverse of this ket as done in the previous section). For illustration purposes, we use Coefficients and note how it automatically expands the commutator
| > |
| (34) |
One can undo this (frequently undesired) expansion of the commutator by sorting the products on the left-hand side using the commutator between ![]() and
and ![]()
| > |
| (35) |
And that is the result we wanted to compute.
Additionally, to see this rule in matrix form,
| > |
 |
(36) |
In the above, we use equation (30) multiplied by -1 to avoid a minus sign in all the elements of (36), due to having worked with the default signature (- - - +); this minus sign is not necessary if in the Setup at the beginning one also sets ![]()
For display purposes, to see this matrix expressed in terms of the geometrical components of the momentum ![]() , redefine the tensor
, redefine the tensor ![]() explicitly indicating its Cartesian component
explicitly indicating its Cartesian component
| > |
| (37) |
| > |
 |
(38) |
Finally, in a typical situation, these commutation rules are to be taken into account in further computations, and for that purpose they can be added to the setup via
| > |
| (39) |
For example, from herein computations are performed taking into account that
| > |
| (40) |
There are 991 metrics in the database of solutions to Einstein's equations, based on the book "Exact solutions to Einstein's equations". One can check this number via
| > |
| (41) |
For the majority of these solutions, the book also presents, explicit or implicitly, the form of the Energy-Momentum tensor. New in Maple 2018, we added to the database one more entry indicating the components of the corresponding EnergyMomentum tensor, covering, in Maple 2018.0, 686 out of these 991 solutions.
The design of the EnergyMomentum tensor got slightly adjusted to take these new database entries into account, so that when you load one of these solutions, if the corresponding entry for the EnergyMomentumTensor is already in the database, it is automatically loaded together with the solution.
In addition, it is now possible to define the tensor components using the Define command, or redefine any of its components using the new Library:-RedefineTensorComponent routine.
Examples
| > |
Consider the metric of Chapter 12, equation number 16.1
| > |
 |
(42) |
New, the covariant components of the EnergyMomentum tensor got automatically loaded, given by
| > |
 |
(43) |
One can verify this checking for the tensor's definition
| > |
![Typesetting:-mprintslash([Physics:-EnergyMomentum[mu, nu] = `+`(`/`(`*`(`/`(1, 8), `*`(Physics:-Einstein[mu, nu])), `*`(Pi))), Physics:-EnergyMomentum[`~mu`, `~nu`] = (Matrix(4, 4, {(1, 1) = Typesetti...](Physics/Physics_182.gif) |
(44) |
Take now the tensor components of the first defining equation of (44)
| > |
 |
(45) |
where ![]() is related to Newton’s constant.
is related to Newton’s constant.
To see the continuity equations for the components of ![]() , use for instance the inert version of the covariant derivative operator D_ and the TensorArray command
, use for instance the inert version of the covariant derivative operator D_ and the TensorArray command
| > |
| (46) |
| > |
 |
(47) |
| > |
| (48) |
The EnergyMomentum tensor can also be (re)defined in any particular way (a correct definition must satisfy ![]() ).
).
Example:
Define the EnergyMomentum tensor indicating the functionality in the definition in terms of ![]() to be constant energy (i.e. no functionality) and the flux density
to be constant energy (i.e. no functionality) and the flux density ![]() and stress
and stress ![]() tensors depending on
tensors depending on ![]() For this purpose, use the new option minimizetensorcomponents to make explicit the symmetry of the stress tensor
For this purpose, use the new option minimizetensorcomponents to make explicit the symmetry of the stress tensor ![]()
| > |
| (49) |
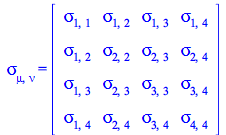
The symmetry of ![]() is now explicit in that its matrix form is symmetric
is now explicit in that its matrix form is symmetric
| > |
 |
(50) |
The new routines for testing tensor symmetries
| > |
| (51) |
The symmetry is regarding interchanging positions of the 1st and 2nd indices
| > |
| (52) |
So this is the form of the EnergyMomentum with all its components - but for the total energy - depending on the coordinates
| > |
 |
(53) |
| > |
| (54) |
Define now ![]() with these components
with these components
| > |
| (55) |
| > |
 |
(56) |
To see the continuity equations for the components of ![]() , use again the inert version of the covariant derivative operator D_ and the TensorArray command
, use again the inert version of the covariant derivative operator D_ and the TensorArray command
| > |
| (57) |
For a more convenient reading, present the result as a vector column
| > |
 |
(58) |
Comparing the specific form (43) for the EnergyMomentum loaded from the database of solutions to Einstein's equations with the general form (56), one can ask the formal question of whether there are other forms for the EnergyMomentum satisfying the continuity equations (58).
To answer that question, rewrite this system of equations for the flux density ![]() and stress
and stress ![]() tensors as a set, and solve it for them
tensors as a set, and solve it for them
| > |
| (59) |
This system in fact admits much more general solutions than (43):
| > |
           |
(60) |
This solution can be verified in different ways, for instance using pdetest showing it cancels the PDE system (59) for ![]() and stress
and stress ![]()
| > |
| (61) |
A new keyword in Define and Setup: minimizetensorcomponents, allows for automatically minimizing the number of tensor components taking into account the tensor symmetries. For example, if a 2-tensor in a 4D spacetime is defined a antisymmetric, the number of different tensor components is 6, and the elements of the diagonal are automatically set equal to 0. After setting this keyword to true with Setup, all subsequent definitions of tensors automatically minimize the number of components while using this keyword with Define makes this minimization only happen with the tensors being defined in the call to Define.
Related to this new functionality, 4 new Library routines were added: MinimizeTensorComponents, NumberOfIndependentTensorComponents, RelabelTensorComponents and RedefineTensorComponents
Example:
| > |
Define an antisymmetric tensor with two indices
| > |
| (62) |
Although the system knows that ![]() is antisymmetric,
is antisymmetric,
| > |
| (63) |
| > |
| (64) |
by default the compotes of ![]() do not automatically reflect that, it is necessary to use the simplifier of the Physics package, Simplify.
do not automatically reflect that, it is necessary to use the simplifier of the Physics package, Simplify.
| > |
| (65) |
| > |
| (66) |
Likewise, computing the array form of ![]() we do not see the elements of the diagonal equal to nor the lower-left triangle equal to the upper-right triangle but with a different sign:
we do not see the elements of the diagonal equal to nor the lower-left triangle equal to the upper-right triangle but with a different sign:
| > |
 |
(67) |
This new functionality, here called minimizetensorcomponents, makes the symmetries of the tensor explicitly reflected in its components. There are three ways to use it. First, one can minimize the number of tensor components of a tensor previously defined. For example
| > |
 |
(68) |
After this, both ![]() and
and ![]() are automatically equal to 0 without having to use Simplify
are automatically equal to 0 without having to use Simplify
| > |
| (69) |
| > |
| (70) |
And the output of TensorArray in ![]() becomes equal to
becomes equal to ![]() .
.
NOTE: after using minimizetensorcomponents in the definition of a tensor, say F, all the keywords implemented for Physics tensors are available for the F:
| > |
 |
(71) |
| > |
| (72) |
| > |
| (73) |
| > |
| (74) |
Alternatively, one can define a tensor, specifying that the symmetries should be taken into account to minimize the number of its components passing the keyword minimizetensorcomponents to Define.
Example:
Define a tensor with the symmetries of the Riemann tensor, that is, a tensor of 4 indices that is symmetric with respect to interchanging the positions of the 1st and 2nd pair of indices and antisymmetric with respect to interchanging the position of its 1st and 2nd indices, or 3rd and 4th indices, and minimizing the number of tensor components
| > |
| (75) |
| > |
| (76) |
| > |
| (77) |
One can always retrieve the symmetry properties in the abstract notation used by the Define command using the new ![]() , its output is ordered, first the symmetric then the antisymmetric properties
, its output is ordered, first the symmetric then the antisymmetric properties
| > |
| (78) |
After making the symmetries explicit (and also before that), it frequently s useful to know the number of independent components of a given tensor. For this purpose use the new ![]()
| > |
| (79) |
and besides the symmetries, in the case of the Riemann tensor after taking into account the first Bianchi identity, this number of components is further reduced to 20.
A third way of using the new minimizetensorcomponents functionality is using Setup, so that every subsequent definition of tensors with symmetries is automatically performed minimizing the number of components.
Example:
| > |
| (80) |
You can now define without having to include the keyword ![]() in the definition of tensors with symmetries
in the definition of tensors with symmetries
| > |
| (81) |
| > |
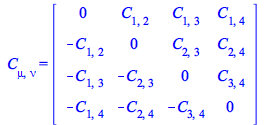 |
(82) |
| > |
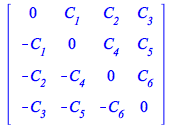 |
(83) |
Suppose now we want to make one of these components equal to 1, say ![]()
| > |
 |
(84) |
New: as part of the developments of Physics bug regardless of loading the Physics package, inert names are now typeset in gray, the standard for inert functions, with copy & paste working
| > |
| > |
| (85) |
| > |
| (86) |
Note that this was already in place in previous releases regarding inert functions but not regarding inert names. Regarding inert functions, since Maple 2016 their typesetting is also in grey with copy & paste working
| > |
| (87) |
Regarding Physics, having the right typeset also for symbols and tensor names is particularly relevant now that one can compute with differential operators as operands of a product.
Example:
| > |
| > |
| (88) |
The active and inert representations of the same differential-vectorial operator are
| > |
| (89) |
Hence, you can:
a) assign a mapping to p_ while represent it using %p_ when you do not want the mapping to be applied.
b) using %p_ has mathematical and clear typesetting (in gray always means inert) making its use more pleasant / easy to read.
Example:
| > |
Assign a procedure to the differential-vectorial operator ![]()
| > |
| (90) |
Apply both the active and the inert operators to some function of the coordinates
| > |
| (91) |
Apply now the differential operators in products: the left-hand side, inert, remains a product, while the right-hand side, becomes a function application, and so ![]() gets applied
gets applied
| > |
| (92) |
NOTE: the implementation is such that if p is noncommutative, then so is %p and the same holds regarding their possibly differential operator and tensorial character: the inert versions inherit the properties of their active counterparts, and the same regarding their tensorial character: if p is a tensor, so is %p. In addition, inert tensors are also now displayed the same way as their active versions but in gray, improving the readability of tensorial expressions
Example:
Load a curved spacetime, for instance Schwarzschild's metric
| > |
 |
(93) |
Define a tensor and compute its covariant derivative equating the inert with the active form of it
| > |
| (94) |
| > |
| (95) |
Since ![]() is a tensor, so is
is a tensor, so is ![]() , and the latter is typeset as the former, only in gray, with copy & paste working, reproducing
, and the latter is typeset as the former, only in gray, with copy & paste working, reproducing ![]()
| > |
| (96) |
| > |
| (97) |
Also new, the same holds for the typesetting of inert differential operators, the inert display of the covariant derivative symbol is now the same as the active one only in gray.
| > |
| (98) |
Expand the right-hand side and replace the active Christoffel by its inert counterpart %Christoffel
| > |
| (99) |
| > |
| (100) |
Compute the components of the left and right hand sides of this tensorial equation, it is a 2x2 matrix of equations; check one of these components: the readability of the inert symbols entering the equation is now straightforward due to the typesetting of inert tensors
| > |
| > |
| (101) |
These expression are not just typeset but true inert representations of the underlying computations. To transform them into active, use value
| > |
| (102) |
New in Maple 2018, the algebra rules for the Dirac, Pauli and Gell-Mann matrices are automatically set when Physics is loaded. This means expressions can be simplified taking into account these algebra rules, which can also be queried using a new Library:-DefaultAlgebraRules routine that returns the algebras in terms of generic lowercase Latin indices
| > |
The algebra rules for all of the Pauli, Dirac and Gell-Mann matrices, in a 4D spacetime, are given according to the value of the signature by
| > |
| (103) |
Simplification of products of Dirac matrices work automatically taking the corresponding (3rd) algebra rule into account; for example (see also next section)
| > |
| (104) |
| > |
| (105) |
| > |
| (106) |
| > |
| (107) |
The convention for ![]() follows the Landau, Bogoliubov and Tong books on quantum fields, so for the default signature
follows the Landau, Bogoliubov and Tong books on quantum fields, so for the default signature
| > |
| (108) |
using the new ![]() routine, we have
routine, we have
| > |
| (109) |
This new ![]() routine takes into account the possibly Euclidean character of spacetime, also the possible values of the signature: (- - - +), (+ - - -), (+ + + -) and (- + + +), and uses formulas valid for the three representations: standard, chiral and majorana.
routine takes into account the possibly Euclidean character of spacetime, also the possible values of the signature: (- - - +), (+ - - -), (+ + + -) and (- + + +), and uses formulas valid for the three representations: standard, chiral and majorana.
The algebra rules now automatically loaded when Physics is loaded can always overwritten. For instance, to represent the algebra of Dirac matrices with an identity matrix on the right-hand side, one can proceed as follows.
First create the identity matrix. To emulate what we do with paper and pencil, where we write to represent an identity matrix without having to see the actual table 2x2 with the number 1 in the diagonal and a bunch of 0, I will use the matrix command, not the Matrix one. One way of entering this identity matrix is
| > |
![Typesetting:-mprintslash([`𝕀` := matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])], [array( 1 .. 4, 1 .. 4, [( 1, 4 ) = (0), ( 2, 3 ) = (0), ( 4, 1 ) = (0), ( 2, 4 ) = (0), ( 3, 3...](Physics/Physics_394.gif) |
(110) |
Depending on the context, the advantage of matrix versus Matrix is that is also of type algebraic
| > |
| (111) |
Consequently, one can operate with it algebraically without displaying its contents (not possible with Matrix)
| > |
| (112) |
Most commands of the library only work with objects of type algebraic, all these will be able to handle this matrix, and the contents is displayed only on demand, for instance using eval
| > |
![Typesetting:-mprintslash([matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])], [array( 1 .. 4, 1 .. 4, [( 1, 4 ) = (0), ( 2, 3 ) = (0), ( 4, 1 ) = (0), ( 2, 4 ) = (0), ( 3, 3 ) = (1), ( ...](Physics/Physics_400.gif) |
(113) |
Set now the algebra for Dirac matrices with an matrix on the right-hand side
| > |
| (114) |
| > |
| (115) |
Verifying
| > |
| (116) |
Set now a Dirac spinor (in a week from today, this will be possible directly using Physics:-Setup, but today, here, I do it step-by-step)
For that you can also use {vector, matrix, array} or {Vector, Matrix, Array}, and again, if you use the Upper case commands, you always have the components visible, and cannot compute with these object using commands that require the input to be of type algebraic. So I use matrix, not Matrix, and matrix instead of vector so that the Dirac spinor that is both algebraic and matrix, is also displayed in the usual display as a "column vector"
To reuse the letter Psi which in Maple represents the Psi function, use a local version of it
| > |
| > |
| (117) |
Specify the components of the spinor, in any preferred way, for example using ![]()
| > |
![Typesetting:-mprintslash([Psi := matrix([[psi[1]], [psi[2]], [psi[3]], [psi[4]]])], [array( 1 .. 4, 1 .. 1, [( 4, 1 ) = (psi[4]), ( 2, 1 ) = (psi[2]), ( 1, 1 ) = (psi[1]), ( 3, 1 ) = (psi[3]) ] )])](Physics/Physics_412.gif) |
(118) |
Check it out:
| > |
| (119) |
| > |
| (120) |
Let’s see all this working together by multiplying the anticommutator equation by ![]()
| > |
| (121) |
To see the matrix form of this equation use the new ![]() routine
routine
| > |
 |
(122) |
Or directly rewrite, then perform, in one go, the matrix operations behind (121)
| > |
 |
(123) |
REMARK: As shown above, in general, the representation using lowercase commands allows you to use `*` or `.` depending on whether you want to represent the operation or perform the operation. For example this represents the operation, as an exact mimicry of what we do with paper and pencil, both regarding input and output
| > |
| (124) |
And this performs the operation
| > |
![Typesetting:-mprintslash([matrix([[psi[1]], [psi[2]], [psi[3]], [psi[4]]])], [array( 1 .. 4, 1 .. 1, [( 4, 1 ) = (psi[4]), ( 2, 1 ) = (psi[2]), ( 1, 1 ) = (psi[1]), ( 3, 1 ) = (psi[3]) ] )])](Physics/Physics_429.gif) |
(125) |
Or to only displaying the operation
| > |
![Typesetting:-mprintslash([Physics:-`.`(matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]), matrix([[psi[1]], [psi[2]], [psi[3]], [psi[4]]]))], [Physics:-`.`(array( 1 .. 4, 1 .. 4, [( 1, ...](Physics/Physics_431.gif) |
(126) |
Finally, another way to visualize the equations behind (121) is
| > |
 |
(127) |
Or additionally performing the matrix operations of each of the equations in (127) using the new option performmatrixoperations of TensorArray
| > |
 |
(128) |
The computation of traces of products of Dirac matrices was implemented years ago - see Physics,Trace.
The simplification of products of Dirac matrices, however, was not. Now in Maple 2018 it is.
| > |
| > |
First of all, when loading Physics, a frequent question is about the signature, the default is (- - - +)
| > |
| (129) |
This is important because the convention for the Algebra of Dirac Matrices depends on the signature. With the signatures (- - - +) as well as (+ - - -), the sign of the timelike component is 1
| > |
| (130) |
With the signatures (+ + + -) as well as (- + + +), the sign of the timelike component is -1
| > |
| (131) |
The simplification of products of Dirac Matrices, illustrated below with the default signature, works fine with any of these signatures, and works without having to set a representation for the Dirac matrices -- all the results are representation-independent.
Consider now the following five products of Dirac matrices
| > |
| (132) |
| > |
| (133) |
| > |
| (134) |
| > |
| (135) |
| > |
| (136) |
New: the simplification of these products is now implemented
| > |
| (137) |
Verify this result performing the underlying matrix operations
| > |
| (138) |
Note that in (138) the right-hand side has no matrix elements. This is standard in particle physics where the computations with Dirac matrices are performed algebraically. For the purpose of actually performing the underlying matrix operations, however, one may want to rewrite the algebra of Dirac matrices including a 4x4 identity matrix. For that purpose, see Algebra of Dirac Matrices with an identity matrix on the right-hand side. For the purpose of this illustration, below we proceed with as shown in (138), interpreting right-hand sides as if they involve an identity matrix.
To verify these results checking the components of the matrices involved we set a representation for the Dirac matrices, for example the standard one
| > |
| (139) |
Verify ![]() using the new
using the new ![]() routine
routine
| > |
 |
(140) |
The same with the other expressions
| > |
| (141) |
| > |
| (142) |
| > |
| (143) |
| > |
 |
(144) |
For e2
| > |
| (145) |
| > |
| (146) |
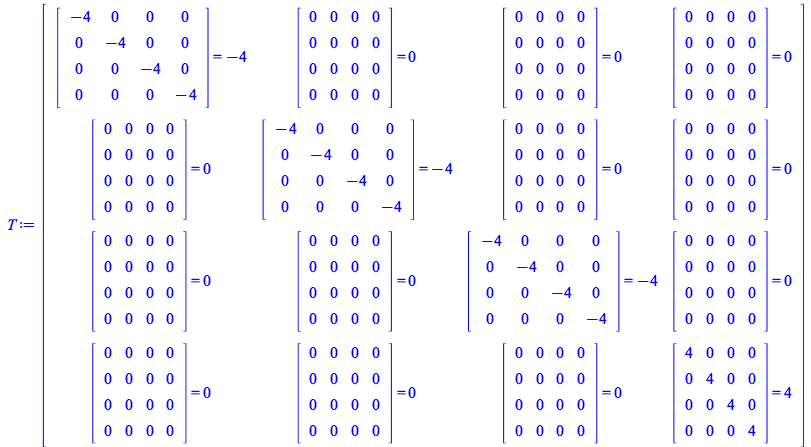
To make the output simpler, use the new option performmatrixoperations of TensorArray, accomplishing two steps in one go
| > |
 |
(147) |
For the other two products of Dirac matrices we have
| > |
| (148) |
| > |
| (149) |
These results can be verified in the same way done for the simplification of e2 and e1, as shown in this page, under Library routines to perform matrix operations in expressions involving spinors with omitted indices
Finally, let's define some tensors and contract their product with these expressions involving products of Dirac matrices.
Example
| > |
| (150) |
Contract with e1 and e2 and simplify
| > |
| (151) |
| > |
| (152) |
New Physics:-Library routines, RewriteInMatrixForm, and PerformMatrixOperations where added, to rewrite or perform the matrix operations implicit in expressions where the spinor indices are omitted. In some sense, the new Library:-PerformMatrixOperations is a Matrix version (or spinor version) of the TensorArray command, which now also has a new option, performmatrixoperations to additionally perform the matrix or spinor operations in expressions
Example:
The computation of traces of products of Dirac matrices was implemented years ago.
The simplification of products of Dirac matrices, however, was not. Now it is.
| > |
Set a representation for the Dirac matrices, say the standard one
| > |
| (153) |
An Array with the four Dirac matrices are
| > |
| (154) |
The definition of the Dirac matrices is implemented in Maple following the conventions of Landau books ([1] Quantum Electrodynamics, V4), and does not depend on the signature, i.e. the form of these matrices is, using the new ![]()
| > |
 |
(155) |
With the default signature (- - - +), the space part components of ![]() change sign when compared with corresponding ones from
change sign when compared with corresponding ones from ![]() while the timelike component remains unchanged
while the timelike component remains unchanged
| > |
| (156) |
| > |
 |
(157) |
With this default signature (- - - +), the algebra of the Dirac Matrices, now loaded by default when Physics is loaded, is (see page 80 of [1])
| > |
| (158) |
You can also display this algebra, with generic indices j, k, using the new Library routine for this purpose
| > |
| (159) |
Verify the algebra rule by performing all the involved matrix operations
| > |
| (160) |
Note that, regarding the spacetime indices, this is a 4x4 matrix, whose elements are in turn 4x4 matrices. Compute first the external 4x4 matrix related to ![]() and
and ![]()
| > |
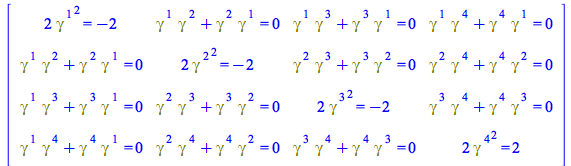 |
(161) |
Perform now all the matrix operations involved in each of the elements of this 4x4 matrix: you can do this by using the new option performmatrixoperations of TensorArray or using the new Library routine for this purpose
| > |
 |
(162) |
By eye everything checks OK. Note as well that in (162) the right-hand sides have no matrix elements. This is standard in particle physics where the computations with Dirac matrices are performed algebraically. For the purpose of actually performing the underlying matrix operations, however, one may want to rewrite this algebra including a 4x4 identity matrix on the right-hand sides. For that purpose, see the MaplePrimes post Algebra of Dirac Matrices with an identity matrix on the right-hand side. For the purpose of this illustration, below we proceed with the algebra as shown in (162), interpreting right-hand sides as if they involve an identity matrix.
Consider now the following five products of Dirac matrices
| > |
| (163) |
| > |
| (164) |
| > |
| (165) |
| > |
| (166) |
| > |
| (167) |
New: the simplification of these products is now implemented
| > |
| (168) |
Verify this result performing the underlying matrix operations
| > |
| (169) |
| > |
 |
(170) |
The same with the other expressions
| > |
| (171) |
| > |
| (172) |
| > |
| (173) |
| > |
 |
(174) |
For e2
| > |
| (175) |
| > |
| (176) |
| > |
| (177) |
| > |
 |
(178) |
For e3 we have
| > |
| (179) |
Verify this result,
| > |
| (180) |
In this case, with three free spacetime indices ![]() , the spacetime components form an array 4x4x4 of 64 components, each of which is a matrix equation
, the spacetime components form an array 4x4x4 of 64 components, each of which is a matrix equation
| > |
![Typesetting:-mprintslash([T := RTABLE(18446744078163780782, anything, Array, rectangular, Fortran_order, [], 3, 1 .. 4, 1 .. 4, 1 .. 4)], [Array(%id = 18446744078163780782)])](Physics/Physics_575.gif) |
(181) |
For instance, the first element is
| > |
| (182) |
and it checks OK:
| > |
 |
(183) |
How can you test the 64 components of T all at once?
1. Compute the matrices, without displaying the whole thing, take the elements of the array and remove the indices (i.e. take the right-hand side); call it M
| > |
For instance,
| > |
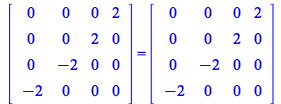 |
(184) |
Now verify all these matrix equations at once: take the elements of the arrays on each side of the equations and verify that the are the same: we expect for output just ![]()
| > |
| (185) |
The same for e4
| > |
| (186) |
| > |
| (187) |
Regarding the spacetime indices this is now an array 4x4x4x4
| > |
![Typesetting:-mprintslash([T := RTABLE(18446744078201340382, anything, Array, rectangular, Fortran_order, [], 4, 1 .. 4, 1 .. 4, 1 .. 4, 1 .. 4)], [Array(%id = 18446744078201340382)])](Physics/Physics_591.gif) |
(188) |
For instance the first of these 256 matrix equations
| > |
| (189) |
verifies OK:
| > |
 |
(190) |
Now all the 256 matrix equations verified at once as done for e3
| > |
| > |
| (191) |
A large number of miscellaneous improvements happened for Physics in Maple 2018. For brevity, these improvements are only listed; among the most relevant ones:
 we now use
we now use  , an upside down triangle that is slightly different from Nabla,
, an upside down triangle that is slightly different from Nabla,  used in Physics:-Vectors.
used in Physics:-Vectors. *Ce programme d'évaluation n'est proposé actuellement ni aux étudiants ni aux particuliers.