|

Chapter 9: Vector Calculus
Section 9.9: Stokes' Theorem

|
Example 9.9.5
|
|
|
Apply Stokes' theorem to the vector field ; the curve , the triangle with vertices ; and the first-octant portion of the plane along with the coordinate planes as the capping surface . Hint: has three sides but is open at the bottom.
|
|
|

|
Solution
|
|

|
Mathematical Solution
|
|
|
•
|
The surface is shown in Figure 9.9.5(a), where outward normal vectors are drawn on each of the three faces , comprising , and listed in Table 9.9.5(a).
|
|
|
first-octant part of the plane
|
|
|
the region in the -plane bounded by the triangle whose vertices are , , and
|
|
|
the region in the - plane bounded by the triangle whose vertices are , , and
|
|
Table 9.9.5(a)
|
|
|
|
|
>
|
use plots,Student:-VectorCalculus in
module()
local p1,p2,p3,p4,p5,N1,N2,N3;
N1:=RootedVector(root=[3,0,3],<0,-1,0>);
N2:=RootedVector(root=[0,2,2],<-1,0,0>);
N3:=RootedVector(root=[3,2,3],<2,3,4>/sqrt(29));
p1:=plot3d(6-x/2-3*y/4,x=0..12,y=0..8-2*x/3,color=red);
p2:=plot3d([x,0,z],x=0..12,z=0..6-x/2,color=gold);
p3:=plot3d([0,y,z],y=0..8,z=0..6-3*y/4,color=green);
p4:=PlotVector([N1,N2,N3],color=black,width=.3);
p5:=display(p1,p2,p3,p4,axes=frame,tickmarks=[3,3,4],labels=[x,y,z],scaling=constrained,style=surface,orientation=[-20,75,0],lightmodel=none);
print(p5);
end module:
end use:
|

|
|
Figure 9.9.5(a) The surface
|
|
|
|
|
|
Begin by calculating
=
A unit (upward) normal on is where . Hence,
and
which, on becomes
The projection of onto the plane is a right triangle whose hypotenuse is , from which it follows that
=
An outward normal on where is the unit vector . Hence, on , a right triangle with hypotenuse in the -plane. This gives the integral
= = 72
An outward normal on where is the unit vector . Hence, on , a right triangle with hypotenuse in the -plane. This gives the integral
= = 64
From these results it follows that = .
The surface caps , the right triangle with vertices . Since this triangle lies in the plane , on each leg, and is on the hypotenuse. See Table 9.9.5(b) for the details.
From Table 9.9.5(b), it follows that = .
|

|
Maple Solution - Interactive
|
|
|
Initialize
|
|
•
|
Tools≻Load Package: Student Vector Calculus
|
|
Loading Student:-VectorCalculus
|
|
•
|
Tools≻Tasks≻Browse: Calculus - Vector≻
Vector Algebra and Settings≻
Display Format for Vectors
|
|
•
|
Press the Access Settings button and select
"Display as Column Vector"
|
|
|
Display Format for Vectors
|
|

|
|
|
|
|
Obtain
|
|
•
|
Control-drag the equation of the plane.
|
|
•
|
Context Panel: Solve≻Obtain Solutions for≻
|
|
•
|
Context Panel: Assign to a Name≻
|
|
|
|
|
Define the vector field F
|
|
•
|
Enter a free vector whose components are those of F.
Context Panel: Evaluate and Display Inline
|
|
•
|
Context Panel: Student Vector Calculus≻Conversions≻To Vector Field
|
|
•
|
Context Panel: Assign to a Name≻F
|
|
|
=
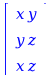
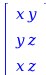
|
|
Obtain
|
|
•
|
Common Symbols palette:
Del and cross-product operators
|
|
•
|
Context Panel: Evaluate and Display Inline
|
|
=
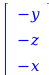
|
|
|
To evaluate , use the task template in Table 9.9.5(c). Should the "Clear All and Reset" button in the Task Template be pressed, all the data that has been input to the template will be lost. In that event, the reader should simply re-launch the example to recover the appropriate inputs to the template.
|
Tools≻Tasks≻Browse:
Calculus - Vector≻Integration≻Flux≻3-D≻Through a Surface Defined over a Triangle
|
|
Flux through a Surface Defined over a Triangle
|
|
|
For the Vector Field:
|
|

|
|
|
|

|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 9.9.5(c) Task template used to evaluate
|
|
|
To evaluate , use the task template in Table 9.9.5(d). Should the "Clear All and Reset" button in the Task Template be pressed, all the data that has been input to the template will be lost. In that event, the reader should simply re-launch the example to recover the appropriate inputs to the template.
|
Tools≻Tasks≻Browse:
Calculus - Vector≻Integration≻Flux≻3-D≻Through a Parametric Surface
|
|
Flux through a Parametrically Defined Surface
|
|
|
For the Vector Field:
|
|

|
|
|
|

|
|

|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 9.9.5(d) Task template used to evaluate
|
|
|
To evaluate , use the task template in Table 9.9.5(e). Should the "Clear All and Reset" button in the Task Template be pressed, all the data that has been input to the template will be lost. In that event, the reader should simply re-launch the example to recover the appropriate inputs to the template.
|
Tools≻Tasks≻Browse:
Calculus - Vector≻Integration≻Flux≻3-D≻Through a Parametric Surface
|
|
Flux through a Parametrically Defined Surface
|
|
|
For the Vector Field:
|
|

|
|
|
|

|
|

|
|
|
|
|
|

|

|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 9.9.5(e) Task template used to evaluate
|
|
|
Unfortunately, Maple takes , not on . Maple's default normal on the open surface described by the position vector is the normalized version of . Since ,
= = = i
Hence, the value of is actually 64, not , and
Table 9.9.4(f) accesses the LineInt command through the Context Panel.
|
Form and evaluate the line integral of F around
|
|
•
|
Write the name F.
Context Panel: Evaluate and Display Inline
|
|
•
|
Context Panel:
Student Vector Calculus≻Line Integral
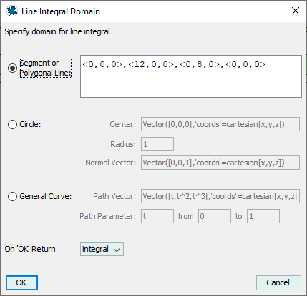
(Complete the dialog as per Figure 9.9.5(b).)
|
|
•
|
Context Panel: Evaluate Integral
|
|
|
|
|
Figure 9.9.5(b) Line Integral Domain dialog
|
|
|
|
|
|
|
|
=
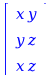
|
|
Table 9.9.5(f) Evaluation of the line integral of F around
|
|
|
Note that in order for Maple to trace the edges of the triangle , the starting vertex must be repeated as the last node to be reached.
|

|
Maple Solution - Coded
|
|
|
Initialize
|
|
•
|
Install the Student VectorCalculus package.
|
|
|
|
|
|
|
|
|
|
Use the Curl and Flux commands to obtain the flux of through
|
|
=
|
|
Use the Curl and Flux commands to obtain the flux of through
|
|
=
|
|
Use the Curl and Flux commands to obtain the flux of through
|
|
=
|
|
|
Unfortunately, Maple takes , not on . Maple's default normal on the open surface described by the position vector is the normalized version of . Since ,
= = = i
Hence, the value of is actually 64, not , and
Table 9.9.5(g) uses the LineInt command to obtain the value of , where is the triangle whose vertices are .
|
=
|
|
Table 9.9.5(g) Line integral of the tangential component of F around
|
|
|
Note that in order for Maple to trace the edges of the triangle , the starting vertex must be repeated as the last node to be reached.
|
|
|
<< Previous Example Section 9.9
Next Example >>
© Maplesoft, a division of Waterloo Maple Inc., 2024. All rights reserved. This product is protected by copyright and distributed under licenses restricting its use, copying, distribution, and decompilation.
For more information on Maplesoft products and services, visit www.maplesoft.com
|
