Étude de Cas :
Transformer l’Enseignement des Mathématiques avec Maple, Maple Learn et la Classe Inversée


Cet article présente la mise en œuvre d’un dispositif d’hybridation pédagogique, centré sur la classe inversée, dans l’enseignement des mathématiques au niveau secondaire au sein d’une classe hétérogène intégrant des élèves bénéficiant de mesures d’aménagements raisonnables. Ce dispositif repose sur une combinaison de ressources numériques variées — capsules vidéo pédagogiques, modules d’auto-évaluation et exercices interactifs dans Maple Learn, ainsi que des exerciseurs à génération aléatoire avec ou sans solution, tirant parti des capacités de Maple. À ces outils numériques s’ajoutent des supports non numériques, tels que des puzzles et des articles scientifiques extraits de magazines, le tout structuré dans un parcours d’apprentissage soigneusement conçu. Le dispositif combine des activités synchrones et asynchrones, appuyées par un forum Teams pour favoriser le soutien collaboratif et les échanges continus. L’approche intègre la différenciation pédagogique, la régulation continue des apprentissages, la création d’exerciseurs adaptatifs avec feedback immédiat et personnalisé, ainsi que des modules de dépassement pour les élèves souhaitant approfondir leur compréhension. L’article explore l’impact de ces éléments sur le développement de l’autonomie, la consolidation des compétences conceptuelles et l’engagement cognitif des élèves en classe, avec pour cas illustratif le théorème de Pythagore.
Dans un contexte d’enseignement européen, les approches hybrides et inversées s’imposent comme des solutions adaptées aux défis d’une éducation inclusive et différenciée. Ces méthodes répondent aux besoins de classes hétérogènes en favorisant l’autonomie des élèves et leur engagement actif.
Dans cette étude, nous nous penchons sur l’intégration des outils Maple et Maple Learn pour concevoir un dispositif innovant. Ce dispositif combine des ressources numériques et non numériques et offre une régulation adaptative des apprentissages.
La problématique au cœur de cet article est la suivante : comment une combinaison de ressources numériques et non numériques peut-elle soutenir l’autonomie, la différenciation et l’engagement des élèves dans une classe de mathématiques hétérogène ?
Cet article présente un dispositif centré sur le théorème de Pythagore, illustrant comment l’hybridation pédagogique peut transformer l’apprentissage des mathématiques.
L’hybridation pédagogique s’inspire des travaux de Marcel Lebrun2, qui mettent en avant l’importance de la classe inversée et de la différenciation pour encourager un apprentissage actif et régulier. Dans ce cadre, la régulation continue des apprentissages est essentielle pour s’adapter aux besoins variés des élèves et garantir leur progression.
Les politiques éducatives européennes soutiennent cette démarche en valorisant le développement des compétences numériques et l’accès à des formats flexibles et inclusifs. Ces fondements ont guidé la conception du dispositif présenté dans cet article.
Population et contexte
La classe compte 30 élèves inscrits en option Mathématiques (6 h/semaine). Elle est hétérogène, avec des niveaux variés, et inclut un groupe bénéficiant d’aménagements raisonnables3.
Chaque étudiant possède un ordinateur portable, une calculatrice scientifique et bénéficie d’une connexion Internet de qualité.
Cette diversité demande une adaptation pédagogique pour garantir l’inclusion et la progression de chacun.
Organisation des séances
Les activités sont structurées pour allier travail synchrone en présentiel et travail asynchrone en autonomie. Le chapitre « Théorème de Pythagore » est programmé sur 4 séances en présentiel, précédées de vidéos explicatives envoyées en amont. Chaque vidéo est accompagnée de petits QCM pour vérifier le visionnage et l’assimilation des concepts de base.
En classe, les élèves travaillent en binômes sur un puzzle mathématique , favorisant la collaboration et l’application concrète des notions abordées. Pour consolider leurs acquis, des modules Maple Learn et Maple sont mis à leur disposition, offrant des exercices interactifs et des opportunités de dépassement pour approfondir la compréhension.
Cette approche hybride permet d’optimiser le temps en présentiel tout en encourageant l’autonomie et l’implication active des élèves.
Méthodes d’évaluation de l’impact du dispositif
L’impact du dispositif est évalué par une combinaison d’exercices en présentiel, d’auto-évaluations et d’un test de synthèse. Lors de chaque séance, 15 minutes sont dédiées à un exercice papier tiré des modules interactifs, corrigé et partagé sur le forum Teams pour ajuster les apprentissages. Les vidéos envoyées en amont, avec QCM intégrés, permettent une auto-évaluation préalable des élèves, tandis que les données des modules Maple Learn et Maple offrent un suivi détaillé de leur progression. Enfin, un test de synthèse sur deux périodes, programmé à la fin du module, permet de mesurer l’acquisition des compétences dans un cadre formel.
Ressources non numériques

Ressources numériques
Ce module de questions à choix multiples vise à repérer la propriété en jeu, avec l’utilisation attendue de la calculatrice pour les calculs intermédiaires.
Ce module de questions exige un développement algébrique rigoureux, permettant de consolider le concept traité.
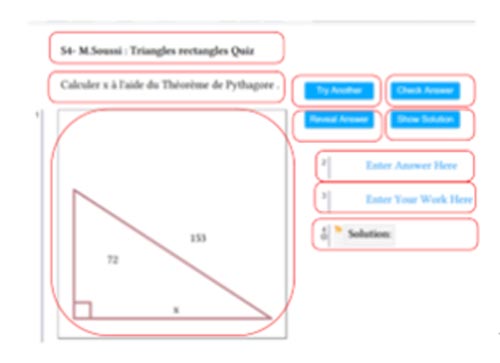
Ce module de questions propose un développement algébrique attendu à partir d’un schéma géométrique donné, favorisant une approche intégrée entre géométrie et algèbre.
Impact sur l’autonomie et l’engagement : Les retours des élèves montrent un renforcement de leur autonomie et de leur engagement grâce aux outils numériques et aux activités proposées. Les vidéos avec QCM favorisent une préparation autonome en amont, leur permettant d’identifier et de combler leurs lacunes avant les séances. Les modules interactifs Maple Learn et Maple offrent un espace d’exploration personnelle, stimulant leur curiosité et leur capacité à approfondir les notions à leur rythme.
En classe, la spontanéité observée dans l’exécution des tâches, notamment lors des puzzles en binômes et des exercices, reflète un intérêt accru pour les activités interactives. Le partage des corrections via Teams renforce cette implication, en encourageant les élèves à utiliser les retours pour progresser. Enfin, le test de synthèse valorise leur travail et couronne un dispositif qui équilibre autonomie et engagement durable.
 Contactez Maplesoft pour savoir comment Maple et Maple Learn peut être utilise pour vas projets
Contactez Maplesoft pour savoir comment Maple et Maple Learn peut être utilise pour vas projets