Example: Monte Carlo Integration |
|
 |
This example implements a Monte-Carlo integrator, and then adds parallelism to the algorithm so that the computation is split over multiple processors when
run on a multi-core computer.
Random values of x can be used to compute an approximation of a definite integral according to the following formula.
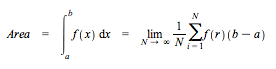
This procedure efficiently calculates a one-variable integral using the above formula where r is a random input to f.
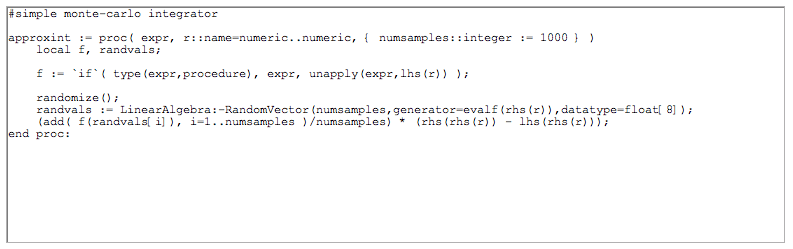
A sample run using 1000 data points shows how this works:

This can be computed exactly in Maple to show the above approximation is rough, but close enough for some applications.

A parallel implementation adds the following code to split the problem over all available nodes and send the partial results back to node 0.
Note that here we are using the head node, 0, to accumulate the results, and not actually do any computations.
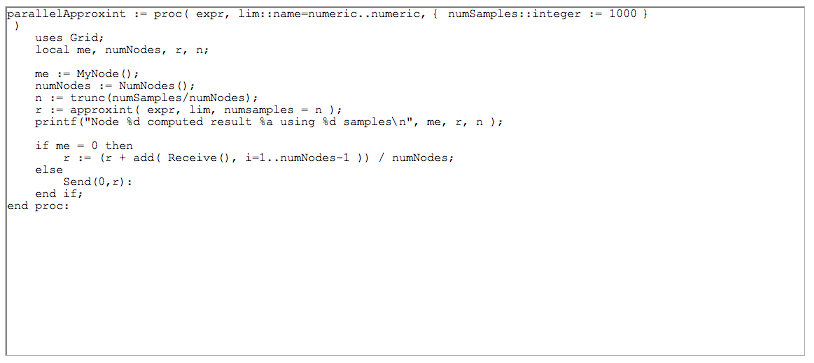
We will integrate over the range, lim, using N samples:
First, do this computation in serial:
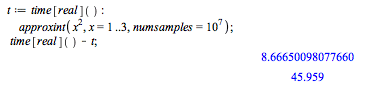
Now, do the same computation in parallel. By default this will spawn one process per core your computer has, possibly adding more for hyperthreading if supported.
You can adjust this using the 'numnodes' option to Launch. This worksheet was run on a computer with two quad-core Intel Xeon E5520 CPUs (8 cores).
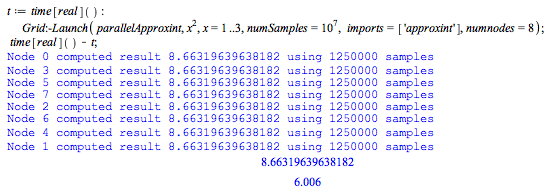
Execution time dropped from 46 seconds to 6 seconds!
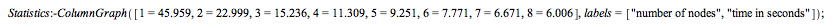
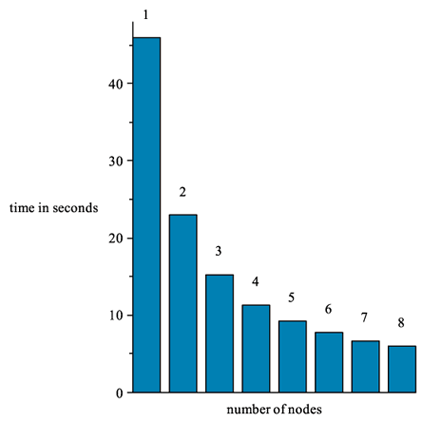
Note that the bar at 8 nodes is roughly 1/8th the height of the bar at 1 node.
If you have Maple 15, you can try the examples on this page yourself:
|
