What is the SIR Model?
The establishment and spread of infectious diseases is a complex phenomenon with many interacting factors, e.g., the environment in which the pathogen and hosts are situated, the population(s) it is exposed to, and the intra- and inter-dynamics of the population it is exposed to. The role of mathematical epidemiology is to model the establishment and spread of pathogens. A predominant method of doing so, is to use the notion of abstracting the population into compartments under certain assumptions, which represent their health status with respect to the pathogen in the system.
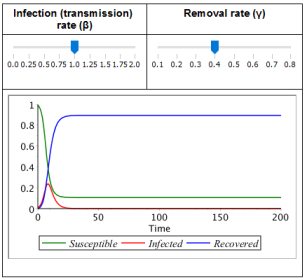
The SIR model labels these three compartments S = number susceptible, I = number infectious, and R = number recovered (immune). This is a good and simple model for many infectious diseases including measles, mumps and rubella.
The letters also represent the number of people in each compartment at a particular time. To indicate that the numbers might vary over time (even if the total population size remains constant), we make the precise numbers a function of t (time): S(t), I(t) and R(t). For a specific disease in a specific population, these functions may be worked out in order to predict possible outbreaks and bring them under control.1
Maple is powerful software for developing and analyzing the SIR model, and for analyzing, exploring, visualizing and solving virtually any mathematical problem. Student pricing available.
Learn more about Maple
Start your free trial
