Etude de cas d’utilisateur :
Maple optimise l’enseignement, motive les étudiants et simplifie l’apprentissage


Défi
Jalal Soussi, un professeur de lycée membre d’un groupe de travail « Transition numérique » en Belgique, souhaitait une solution en mesure d’optimiser l’enseignement et permettant aux enseignants et aux étudiants d’optimiser le temps et les ressources.
Solution
Jalal Soussi a mené des recherches sur les possibilités de Maple afin d’évaluer la capacité de Maple à engager les étudiants et à simplifier le processus d’apprentissage. Il a développé une application mathématique pour illustrer les possibilités de Maple en résolvant divers problèmes.
Résultat
Jalal Soussi a constaté que Maple constituait un environnement idéal pour la création de parcours éducatifs personnalisés pour les étudiants, en raison de sa convivialité et de sa facilité d’exploration leur permettant d’approfondir leur compréhension des concepts clés.
Les outils modernes d’enseignement numérique sont en train de transformer les modes d’éducation en offrant de nouvelles méthodes pour rendre l’apprentissage plus efficace et plus bénéfique pour les étudiants tout en permettant aux enseignants de maximiser le temps et les ressources. Jalal Soussi, un professeur de lycée en Belgique, a mené des recherches sur les capacités de Maple en termes d’optimisation de l’enseignement et a récemment présenté ses conclusions.
Outre sa fonction de professeur de lycée, Jalal Soussi fait également office de formateur dans le domaine de l’Apprentissage des langues assisté par ordinateur (ALAO) et est membre du groupe de travail « Transition numérique » dans le cadre, en Belgique, du Pacte pour un Enseignement d’excellence. Jalal Soussi a beaucoup travaillé avec Maple et s’est récemment penché sur l’utilisation du logiciel pour un « Enseignement d’optimisation » basée sur une série d’applications mathématiques qu’il a développée. Les recherches de Jalal Soussi ont évalué la capacité de Maple à motiver les étudiants et à simplifier l’apprentissage, modifiant par conséquent l’optimisation de l’apprentissage. Selon Jalal Soussi, les différents aspects de la technologie Maplesoft permettent d’atteindre cet objectif, sans oublier :
Jalal Soussi a choisi Maple car c’est un outil logiciel mathématique complet, doté de capacités de calcul formel offrant des solutions précises à de nombreux problèmes. En outre, Maple est également un puissant outil de calcul numérique disposant de fonctionnalités avancées, dont notamment des interfaces 2D et 3D interactives pour la visualisation graphique, l’audio et la vidéo, explique-t-il. « Ses packs, Applications mathématiques et Tutoriels, lui permettent d’aborder, illustrer, formuler des hypothèses, démontrer et comprendre plusieurs concepts mathématiques ».
Jalal Soussi indique que Maple réunit toutes les qualités requises pour expérimenter les mathématiques (c’est-à-dire pour aborder cette discipline de manière originale et stimulante, favorable aux découvertes et intuitions). « Maple est facile à apprendre, et l’aide en ligne, comme par exemple les tutoriels disponibles en permanence, vous dispense pratiquement de consulter le manuel de l’utilisateur », explique-t-il.
Voici un exemple d’application mathématique développée par Jalal Soussi qui illustre les possibilités de Maple.
Problème
Afin d’examiner une séquence pédagogique d’optimisation dans Maple, Jalal Soussi a choisi 20 problèmes variés, en se servant du problème suivant en guise de ligne directrice : « Trouver les dimensions du cylindre circulaire de volume maximal pouvant être inscrit dans une sphère de rayon 4 ».
Jalal Soussi a choisi la structure proposée en raison de sa souplesse, lui permettant d’explorer les différents environnements Maple. En cours de préparation, il s’est consacré aux propriétés géométriques de base du cylindre (Figure 1), en se basant sur le guidage vocal, pour obtenir différentes formules (volume, surface, etc.).
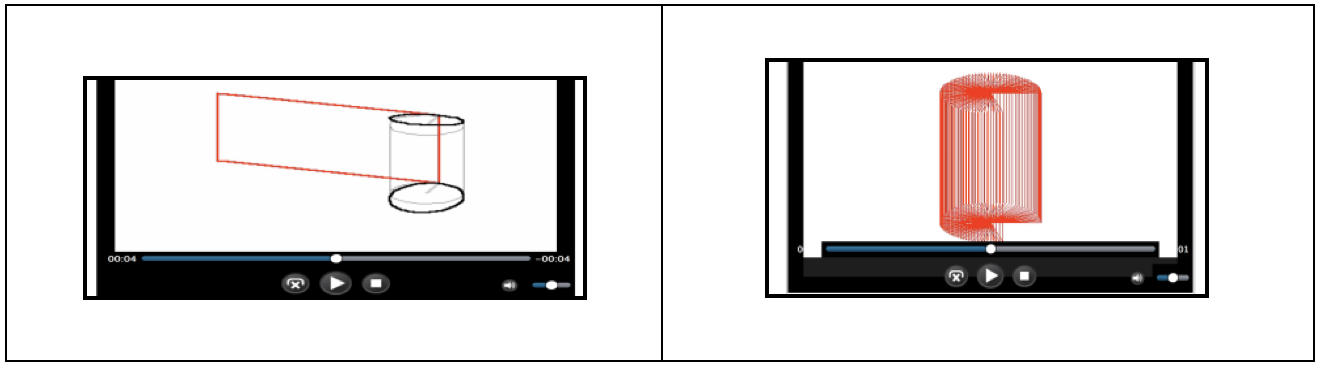
Figure 1
Il a travaillé de manière interactive sur le concept de révolution solide, générée par la rotation de la fonction constante autour de l’axe. Il a ainsi eu l’occasion d’aborder le concept de calcul intégral en face-à-face, sans examen approfondi (Figure 2).
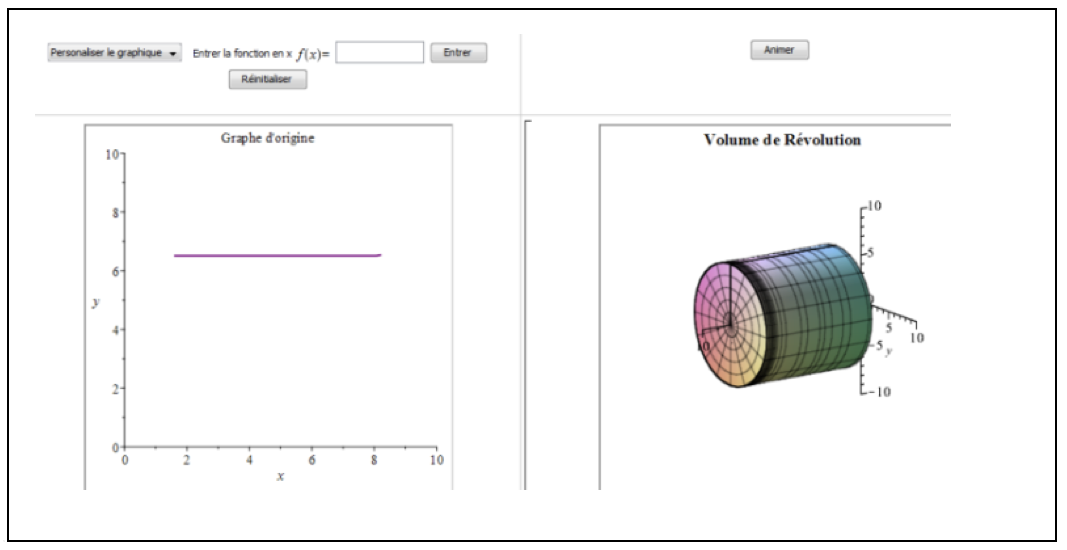
Figure 2
Jalal Soussi renvoie ensuite les utilisateurs vers une autre application reliant les deux figures du problème. En approchant interactivement le volume d’une sphère par les cylindres, les utilisateurs sont à même d’aborder de façon pratique et efficace des concepts tels que les limites et la convergence des séries.
Résolution du problème
Afin de résoudre le problème, les utilisateurs peuvent recourir à plusieurs approches différentes. Les techniques suivantes sont celles proposées par Jalal Soussi dans ses recherches.
Animation dynamique
Les utilisateurs peuvent créer plusieurs figures mobiles en 3D, contrôlées par les différentes variables du problème (hauteur et rayon du cylindre dans le cas du problème pris comme exemple) (Figure 3). On peut ainsi améliorer la perception spatiale de ces représentations.

Figure 3
Essais et erreurs
Jalal Soussi présente la possibilité d’associer les figures dynamiques à un tableau de valeurs (Figure 4). Il a constaté qu’en contrôlant interactivement les variables du problème, l’apprenant est capable de s’approcher numériquement de la solution optimale.
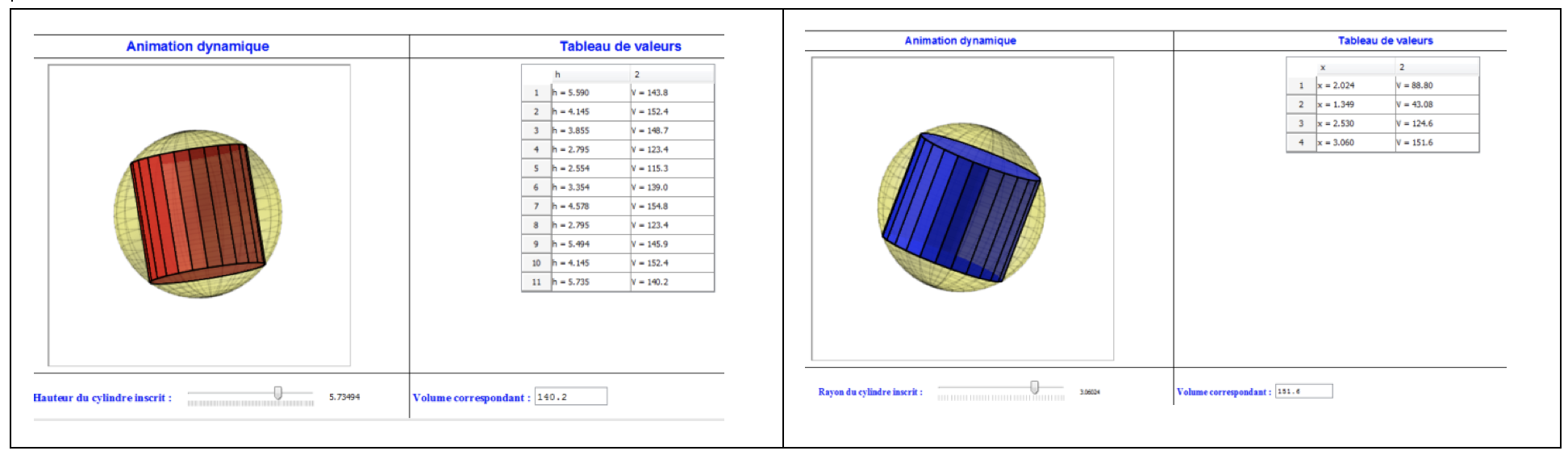
Figure 4
Développement analytique
Jalal Soussi indique que l’analyse minutieuse de la/des fonction(s) d’optimisation (champ de définition, dérivées, monotonie, points remarquables, courbe) s’effectue quelle que soit la forme de la fonction, soit en appelant les commandes Maple (pour les apprenants familiarisés avec le logiciel), soit par le processus intuitif des Mathématiques Cliquables, un concept exclusif de Maple simplifiant le processus pour les néophytes. L’outil « Tutoriels » vous permet de vérifier les différents résultats en toute autonomie (Figures 5-A et 5-B).

Figure 5-A
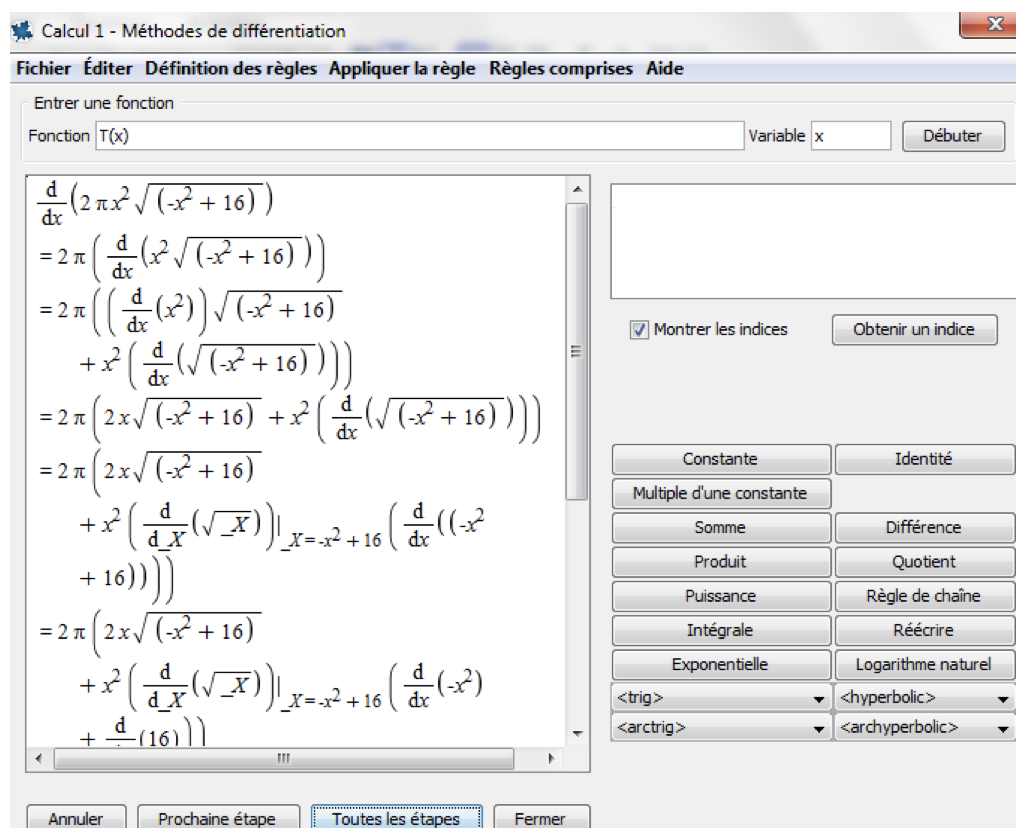
Figure 5-B
A titre d’exemple, Jalal Soussi fournit la fonction d’optimisation suivante, résultant du choix d’agir sur le rayon du cylindre :
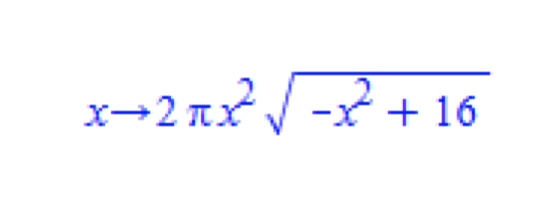
Il donne les exemples suivants de passages croisés :
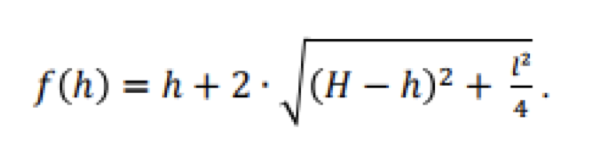

Plusieurs approches différentes faciles à explorer avec Maple sont possibles, souligne Jalal Soussi. L’élévation au carré de la fonction, puis le contrôle graphique et analytique que son maximum se produit au même point que le maximum de sa fonction constituent un bel exemple de cette approche (Figures 6-A et 6-B).

Figure 6-A
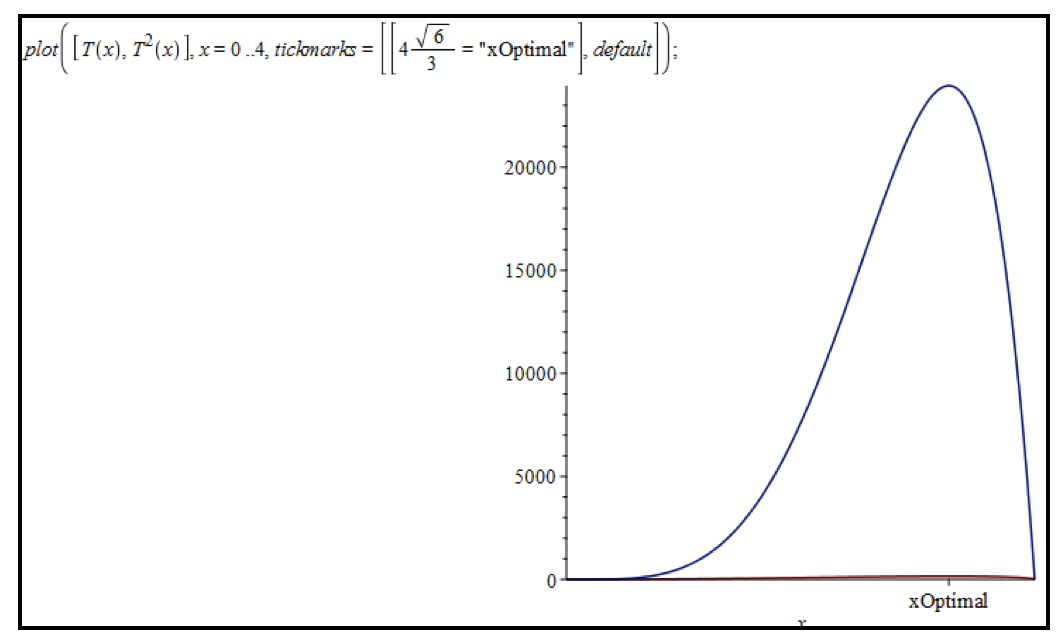
Figure 6-B
Synthèse visuelle
Le graphe d’une fonction est souvent perçu comme un objet statique et son lien avec un phénomène n’est évidemment pas facile à établir pour un apprenant, confie Jalal Soussi. « La multitude de composants interactifs permet aux utilisateurs d’agir interactivement sur les nombreuses variables du problème pour illustrer simultanément plusieurs concepts : la tangente (au niveau de la fonction), le signe (au premier niveau de la dérivée) et la concavité (au deuxième niveau de la dérivée) » On peut le voir sur la Figure 7 ci-dessous.
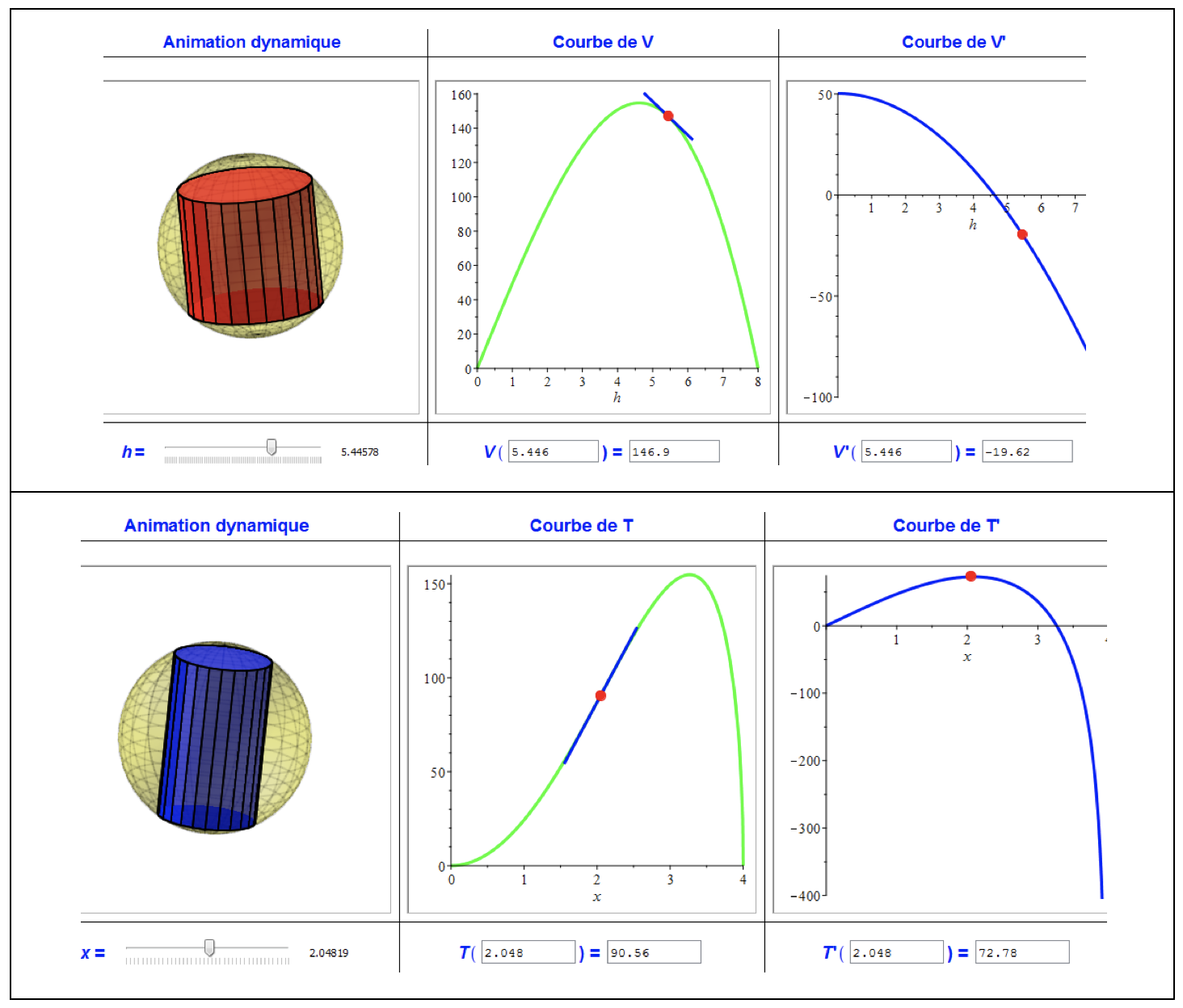
Figure 7
« Le vidéo Optimisation avec Maple, créé par Soussi, montre certaines des façons dont il utilise Maple. »
Conclusion
Afin de maîtriser cette discipline, Jalal Soussi dit qu’il est indispensable de travailler sur tous les problèmes de façon autonome. Jalal Soussi, qui a essayé d’autres logiciels pour aborder un problème de manière identique, estime que Maple constitue une solution idéale. « En effet, lorsqu’on est confronté à des situations similaires, la plupart des manuels et des matériels de soutien pédagogique interrompent l’exploration », conclut-il. « Mais avec Maple, l’apprenant peut facilement explorer ces concepts en profondeur et optimiser son apprentissage ! ».
 Contactez Maplesoft pour savoir comment Maple peut être utilise pour vas projets
Contactez Maplesoft pour savoir comment Maple peut être utilise pour vas projets
Produits
Secteur industriel/Domaine d’application